1.深度优先搜索介绍图的深度优先搜索(DepthFirstSearch)，和树的先序遍历比较类似。它的思想
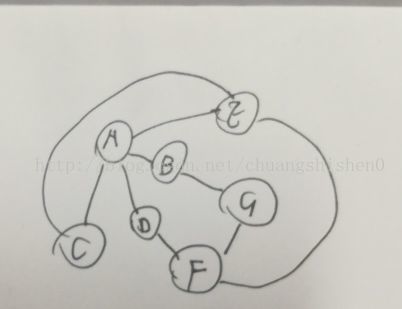
1. 深度优先搜索介绍
图的深度优先搜索(Depth First Search)，和树的先序遍历比较类似。
它的思想：假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。
显然，深度优先搜索是一个递归的过程。
2. 广度优先搜索介绍
广度优先搜索算法(Breadth First Search)，又称为"宽度优先搜索"或"横向优先搜索"，简称BFS。
它的思想是：从图中某顶点v出发，在访问了v之后依次访问v的各个未曾访问过的邻接点，然后分别从这些邻接点出发依次访问它们的邻接点，并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问，直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问，则需要另选一个未曾被访问过的顶点作为新的起始点，重复上述过程，直至图中所有顶点都被访问到为止。
换句话说，广度优先搜索遍历图的过程是以v为起点，由近至远，依次访问和v有路径相通且路径长度为1,2...的顶点。
# -*- coding: utf-8 -*-
"""
Created on Wed Sep 27 00:41:25 2017
@author: my
"""
from collections import OrderedDict
class graph:
nodes=OrderedDict({})#有序字典
def toString(self):
for key in self.nodes:
print key+'邻接点为'+str(self.nodes[key].adj)
def add(self,data,adj,tag):
n=Node(data,adj)
self.nodes[tag]=n
for vTag in n.adj:
if self.nodes.has_key(vTag) and tag not in self.nodes[vTag].adj:
self.nodes[vTag].adj.append(tag)
visited=[]
def dfs(self,v):
if v not in self.visited:
self.visited.append(v)
print v
for adjTag in self.nodes[v].adj:
self.dfs(adjTag)
visited2=[]
def bfs(self,v):
queue=[]
queue.insert(0,v)
self.visited2.append(v)
while(len(queue)!=0):
top=queue[len(queue)-1]
for temp in self.nodes[top].adj:
if temp not in self.visited2:
self.visited2.append(temp)
queue.insert(0,temp)
print top
queue.pop()
class Node:
data=0
adj=[]
def __init__(self,data,adj):
self.data=data
self.adj=adj
g=graph()
g.add(0,['e','c'],'a')
g.add(0,['a','g'],'b')
g.add(0,['a','e'],'c')
g.add(0,['a','f'],'d')
g.add(0,['a','c','f'],'e')
g.add(0,['d','g','e'],'f')
g.add(0,['b','f'],'g')
g.toString()
print '深度优先遍历的结构为'
g.dfs('c')
print '广度优先遍历的结构为'
g.bfs('c')