k-近邻算法是基本的机器学习算法,算法的原理非常简单:
输入样本数据后,计算输入样本和参考样本之间的距离,找出离输入样本距离最近的k个样本,找出这k个样本中出现频率最高的类标签作为输入样本的类标签,很直观也很简单,就是和参考样本集中的样本做对比。下面讲一讲用python实现kNN算法的方法,这里主要用了python中常用的numpy模块,采用的数据集是来自UCI的一个数据集,总共包含1055个样本,每个样本有41个real的属性和一个类标签,包含两类(RB和NRB)。我选取800条样本作为参考样本,剩下的作为测试样本。
下面是分类器的python代码:
'''
kNNClassify(inputAttr, trainSetPath = '', lenOfInstance = 42, startAttr = 0, stopAttr = 40, posOfClass = 41, numOfRefSamples = 5)函数
参数:
inputAttr:输入的属性向量
trainSetPath:字符串,保存训练样本的路径
lenOfInstance:样本向量的维数
startAttr:属性向量在整个样本向量中的起始下标
stopAttr:属性向量在整个样本向量中的终止下标
posOfClass:类标签的在整个样本向量中的下标
numOfClSamples:选出来进行投票的样本个数
返回值:
类标签
'''
def kNNClassify(inputAttr, trainSetPath = '', lenOfInstance = 42, startAttr = 0, stopAttr = 40, posOfClass = 41, numOfRefSamples = 5):
fr = open(trainSetPath)
strOfLine = fr.readline()
arrayOfLine = numpy.array([0.] * lenOfInstance)
refSamples = numpy.array([[-1., 0.]] * numOfRefSamples)
#找出属性中的最大值和最小值,用于归一化
maxAttr, minAttr = kNNFunction.dataNorm(trainSetPath = trainSetPath, lenOfInstance = lenOfInstance)
maxAttr = maxAttr[(numpy.array(range(stopAttr - startAttr + 1))
+ numpy.array([startAttr] * (stopAttr - startAttr + 1)))]
minAttr = minAttr[(numpy.array(range(stopAttr - startAttr + 1))
+ numpy.array([startAttr] * (stopAttr - startAttr + 1)))]
attrRanges = maxAttr - minAttr
inputAttr = inputAttr[(numpy.array(range(stopAttr - startAttr + 1))
+ numpy.array([startAttr] * (stopAttr - startAttr + 1)))]
inputAttr = (inputAttr - minAttr) / attrRanges #归一化
#将字符串转换为向量并进行计算找出离输入样本距离最近的numOfRefSamples个参考样本
while strOfLine != '' :
strOfLine = strOfLine.strip()
strOfLine = strOfLine.split(';')
abandonOrNot = False
for i in range(lenOfInstance) :
if strOfLine[i] == 'RB' :
arrayOfLine[i] = 1.0
elif strOfLine[i] == 'NRB' :
arrayOfLine[i] = 0.0
elif strOfLine[i] != '?' : #没有发现缺失值
arrayOfLine[i] = float(strOfLine[i])
abandonOrNot = False
else : #发现缺失值
abandonOrNot = True
break
if abandonOrNot == True :
strOfLine = fr.readline()
continue
else :
attr = arrayOfLine[(numpy.array(range(stopAttr - startAttr + 1))
+ numpy.array([startAttr] * (stopAttr - startAttr + 1)))]
attr = (attr - minAttr) / attrRanges #归一化
classLabel = arrayOfLine[posOfClass]
distance = (attr - inputAttr) ** 2
distance = distance.sum(axis = 0)
distance = distance ** 0.5
disAndLabel = numpy.array([distance, classLabel])
refSamples = kNNFunction.insertItem(refSamples, numOfRefSamples, disAndLabel)
strOfLine = fr.readline()
continue
#统计每个类标签出现的次数
classCount = {}
for i in range(numOfRefSamples) :
voteLabel = refSamples[i][1]
classCount[voteLabel] = classCount.get(voteLabel, 0) + 1
sortedClassCount = sorted(classCount.iteritems(), key = operator.itemgetter(1), reverse = True)
return int(sortedClassCount[0][0])实现步骤为:读取一条样本,转换为向量,计算这条样本与输入样本的距离,将样本插入到refSamples数组中,当然这里的样本只是一个包含两个元素的数组(距离和类标签),而refSamples数组用于保存离输入样本最近的numOfRefSamples个参考样本。当所有样本都读完之后,就找出了离输入样本最近的numOfRefSamples个参考样本。其中kNNFunction.insertItem函数实现的是将得到的新样本插入到refSamples数组中,主要采用类似冒泡排序的方法,实现代码如下:
'''
insertItem(refSamples, numOfRefSamples, disAndLabel)函数
功能:
在参考样本集中插入新样本,这里的样本是一个包含两个数值的list,第一个是距离,第二个是类标签
在参考样本集中按照距离从小到大排列
参数:
refSamples:参考样本集
numOfRefSamples:参考样本集中的样本总数
disAndLabel:需要插入的样本数
'''
def insertItem(refSamples, numOfRefSamples, disAndLabel):
if (disAndLabel[0] < refSamples[numOfRefSamples - 1][0]) or (refSamples[numOfRefSamples - 1][0] < 0) :
refSamples[numOfRefSamples - 1] = disAndLabel
for i in (numpy.array([numOfRefSamples - 2] * (numOfRefSamples - 1)) - numpy.array(range(numOfRefSamples -1))) :
if (refSamples[i][0] > refSamples[i + 1][0]) or (refSamples[i][0] < 0) :
tempSample = list(refSamples[i])
refSamples[i] = refSamples[i + 1]
refSamples[i + 1] = tempSample
else :
break
return refSamples
else :
return refSamples另外,需要注意的一点是要对输入样本的各条属性进行归一化处理。毕竟不同的属性的取值范围不一样,取值范围大的属性在计算距离的过程中所起到的作用自然就要大一些,所以有必要把所有属性映射到0和1之间。这就需要计算每个属性的最大值和最小值,方法就是遍历整个参考样本集,找出最大值和最小样本,这里用dataNorm函数是实现:
'''
归一化函数,返回归一化向量
'''
def dataNorm(trainSetPath = '', lenOfInstance = 42):
fr = open(trainSetPath)
strOfLine = fr.readline() #从文件中读取的一行字符串
arrayOfLine = numpy.array([0.] * lenOfInstance) #用来保存与字符串对应的数组
maxAttr = numpy.array(['NULL'] * lenOfInstance) #用来保存每条属性的最大值
minAttr = numpy.array(['NULL'] * lenOfInstance) #用来保存每条属性的最小值
while strOfLine != '' :
strOfLine = strOfLine.strip() #去掉字符串末尾的换行符
strOfLine = strOfLine.split(';') #将字符串按逗号分割成字符串数组
abandonOrNot = False
for i in range(lenOfInstance) :
if strOfLine[i] == 'RB' :
arrayOfLine[i] = 1.0
elif strOfLine[i] == 'NRB' :
arrayOfLine[i] = 0.0
elif strOfLine[i] != '?' : #没有发现缺失值
arrayOfLine[i] = float(strOfLine[i])
abandonOrNot = False
else : #发现缺失值
abandonOrNot = True
break
if abandonOrNot == True : #存在缺失值,丢弃
strOfLine = fr.readline()
continue
else : #没有缺失值,保留
if maxAttr[0] == 'NULL' or minAttr[0] == 'NULL' : #maxAttr和minAttr矩阵是空的
maxAttr = numpy.array(arrayOfLine)
minAttr = numpy.array(arrayOfLine)
strOfLine = fr.readline()
continue
for i in range(lenOfInstance) :
if maxAttr[i] < arrayOfLine[i] :
maxAttr[i] = float(arrayOfLine[i])
if minAttr[i] > arrayOfLine[i] :
minAttr[i] = float(arrayOfLine[i])
strOfLine = fr.readline()
continue
return maxAttr, minAttr至此为止,分类器算是完成,接下去就是用剩下的测试集进行测试,计算分类的准确度,用kNNTest函数实现:
def kNNTest(testSetPath = '', trainSetPath = '', lenOfInstance = 42, startAttr = 0, stopAttr = 40, posOfClass = 41):
fr = open(testSetPath)
strOfLine = fr.readline()
arrayOfLine = numpy.array([0.] * lenOfInstance)
succeedClassify = 0.0
failedClassify = 0.0
while strOfLine != '' :
strOfLine = strOfLine.strip()
strOfLine = strOfLine.split(';')
abandonOrNot = False
for i in range(lenOfInstance) :
if strOfLine[i] == 'RB' :
arrayOfLine[i] = 1.0
elif strOfLine[i] == 'NRB' :
arrayOfLine[i] = 0.0
elif strOfLine[i] != '?' : #没有发现缺失值
arrayOfLine[i] = float(strOfLine[i])
abandonOrNot = False
else : #发现缺失值
abandonOrNot = True
break
if abandonOrNot == True :
strOfLine = fr.readline()
continue
else :
inputAttr = numpy.array(arrayOfLine)
classLabel = kNNClassify(inputAttr, trainSetPath = trainSetPath, lenOfInstance = 42, startAttr = startAttr,
stopAttr = stopAttr, posOfClass = posOfClass)
if classLabel == arrayOfLine[posOfClass] :
succeedClassify = succeedClassify + 1.0
else :
failedClassify = failedClassify + 1.0
strOfLine = fr.readline()
accuracy = succeedClassify / (succeedClassify + failedClassify)
return accuracy最后,进行测试:
accuracy = kNN.kNNTest(testSetPath = 'D:\\python_project\\test_data\\QSAR-biodegradation-Data-Set\\biodeg-test.csv',
trainSetPath = 'D:\\python_project\\test_data\\QSAR-biodegradation-Data-Set\\biodeg-train.csv',
startAttr = 0, stopAttr = 40)
print '分类准确率为:',accuracy输出结果为:
分类准确率为: 0.847058823529
可见用kNN这种分类器的对这个数据集的分类效果其实还是比较一般的,而且根据我的测试,分类函数kNNClassify中numOfRefSamples(其实就是k-近邻中k)的取值对分类准确度也有明显的影响,大概在k取5的时候,分类效果比较理想,并不是越大越好。下面谈谈我对这个问题的理解:
首先,kNN算法是一种简单的分类算法,不需要任何训练过程,在样本数据的结构比较简单边界比较明显的时候,它的分类效果是比较理想的,比如:
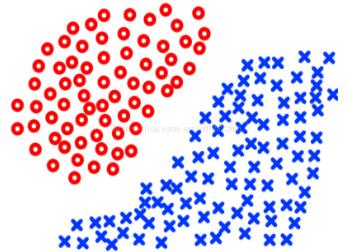
当k的取值比较大的时候,在某些复杂的边界下会出现很差的分类效果,比如下面的情况下很多蓝色的类会被分到红色中,所以要用比较小的k才会有相对较好的分类效果:
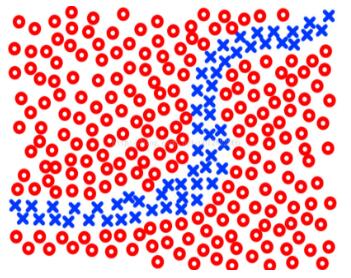
但是当k取得太小也会使分类效果变差,比如当不同类的样本数据之间边界不明显,存在交叉的时候,比如:
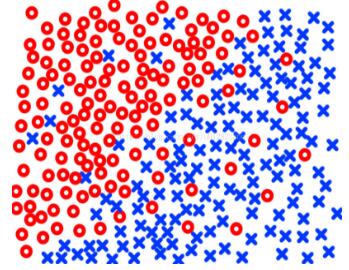
总的来说,kNN分类算法是一种比较原始直观的分类算法,对某些简单的情况有比较好的分类效果,并且不需要训练模型。但是它的缺点是分类过程的运算复杂度很高,而且当样本数据的结构比较复杂的时候,它的分类效果不理想。用kNN算法对本次实验中的数据集的分类效果也比较一般,不过我试过其它更简单一些的数据集,确实还是会有不错的分类准确性的,这里就不赘述了。
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持脚本之家。