本文实例讲述了PHP实现二叉树深度优先遍历(前序、中序、后序)和广度优先遍历(层次)。分享给大家供大家参考,具体如下:
前言:
深度优先遍历:对每一个可能的分支路径深入到不能再深入为止,而且每个结点只能访问一次。要特别注意的是,二叉树的深度优先遍历比较特殊,可以细分为先序遍历、中序遍历、后序遍历。具体说明如下:
前序遍历:根节点->左子树->右子树 中序遍历:左子树->根节点->右子树 后序遍历:左子树->右子树->根节点
广度优先遍历:又叫层次遍历,从上往下对每一层依次访问,在每一层中,从左往右(也可以从右往左)访问结点,访问完一层就进入下一层,直到没有结点可以访问为止。
例如对于一下这棵树:
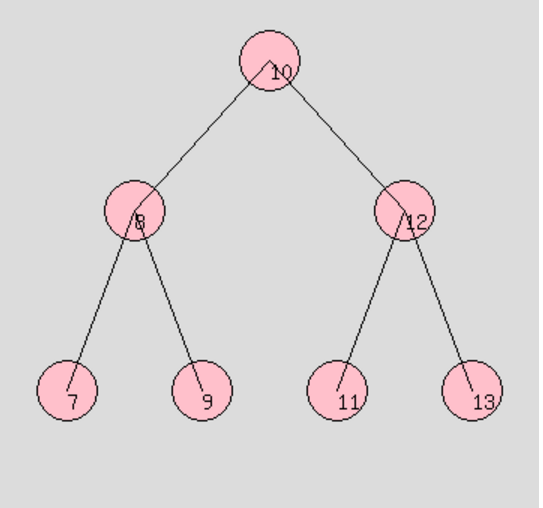
深度优先遍历:
前序遍历:10 8 7 9 12 11 13 中序遍历:7 8 9 10 11 12 13 后序遍历:7 9 8 11 13 12 10
广度优先遍历:
层次遍历:10 8 12 7 9 11 13
二叉树的深度优先遍历的非递归的通用做法是采用栈,广度优先遍历的非递归的通用做法是采用队列。
深度优先遍历:
1、前序遍历:
/**
* 前序遍历(递归方法)
*/
private function pre_order1($root)
{
if (!is_null($root)) {
//这里用到常量__FUNCTION__,获取当前函数名,好处是假如修改函数名的时候,里面的实现不用修改
$function = __FUNCTION__;
echo $root->key . " ";
$this->$function($root->left);
$this->$function($root->right);
}
}
/**
* 前序遍历(非递归方法)
* 因为当遍历过根节点之后还要回来,所以必须将其存起来。考虑到后进先出的特点,选用栈存储。
*/
private function pre_order2($root)
{
// $stack = new splstack();
// $stack->push($root);
// while(!$stack->isEmpty()){
// $node = $stack->pop();
// echo $node->key.' ';
// if(!is_null($node->right)){
// $stack->push($node->right);
// }
// if(!is_null($node->left)){
// $stack->push($node->left);
// }
// }
if (is_null($root)) {
return;
}
$stack = new splstack();
$node = $root;
while (!is_null($node) || !$stack->isEmpty()) {
while (!is_null($node)) {
//只要结点不为空就应该入栈保存,与其左右结点无关
$stack->push($node);
echo $node->key . ' ';
$node = $node->left;
}
$node = $stack->pop();
$node = $node->right;
}
}
//前序遍历
public function PreOrder()
{
// 所在对象中的tree属性保存了一个树的引用
// $this->pre_order1($this->tree->root);
$this->pre_order2($this->tree->root);
}
说明:1、我将所有的遍历方法都封装在一个类 traverse 里面了。2、pre_order2方法中,在使用栈的过程中,我使用的是PHP标准库SPL提供的splstack,如果你们习惯使用数组的话,可以使用 array_push() 和array_pop() 模拟实现。
2、中序遍历:
/**
* 中序遍历(递归方法)
*/
private function mid_order1($root)
{
if (!is_null($root)) {
$function = __FUNCTION__;
$this->$function($root->left);
echo $root->key . " ";
$this->$function($root->right);
}
}
/**
* 中序遍历(非递归方法)
* 因为当遍历过根节点之后还要回来,所以必须将其存起来。考虑到后进先出的特点,选用栈存储。
*/
private function mid_order2($root)
{
if (is_null($root)) {
return;
}
$stack = new splstack();
$node = $root;
while (!is_null($node) || !$stack->isEmpty()) {
while (!is_null($node)) {
$stack->push($node);
$node = $node->left;
}
$node = $stack->pop();
echo $node->key . ' ';
$node = $node->right;
}
}
//中序遍历
public function MidOrder()
{
// $this->mid_order1($this->tree->root);
$this->mid_order2($this->tree->root);
}
3、后序遍历:
/**
* 后序遍历(递归方法)
*/
private function post_order1($root)
{
if (!is_null($root)) {
$function = __FUNCTION__;
$this->$function($root->left);
$this->$function($root->right);
echo $root->key . " ";
}
}
/**
* 后序遍历(非递归方法)
* 因为当遍历过根节点之后还要回来,所以必须将其存起来。考虑到后进先出的特点,选用栈存储。
* 由于在访问了左子节点后怎么跳到右子节点是难点,这里使用一个标识lastVisited来标识上一次访问的结点
*/
private function post_order2($root)
{
if (is_null($root)) {
return;
}
$node = $root;
$stack = new splstack();
//保存上一次访问的结点引用
$lastVisited = NULL;
$stack->push($node);
while(!$stack->isEmpty()){
$node = $stack->top();//获取栈顶元素但不弹出
if(($node->left == NULL && $node->right == NULL) || ($node->right == NULL && $lastVisited == $node->left) || ($lastVisited == $node->right)){
echo $node->key.' ';
$lastVisited = $node;
$stack->pop();
}else{
if($node->right){
$stack->push($node->right);
}
if($node->left){
$stack->push($node->left);
}
}
}
}
//后序遍历
public function PostOrder()
{
// $this->post_order1($this->tree->root);
$this->post_order2($this->tree->root);
}
广度优先遍历:
1、层次遍历:
/**
* 层次遍历(递归方法)
* 由于是按层逐层遍历,因此传递树的层数
*/
private function level_order1($root,$level){
if($root == NULL || $level < 1){
return;
}
if($level == 1){
echo $root->key.' ';
return;
}
if(!is_null($root->left)){
$this->level_order1($root->left,$level - 1);
}
if(!is_null($root->right)){
$this->level_order1($root->right,$level - 1);
}
}
/**
* 层次遍历(非递归方法)
* 每一层从左向右输出
元素需要储存有先进先出的特性,所以选用队列存储。
*/
private function level_order2($root){
if(is_null($root)){
return;
}
$node = $root;
//利用队列实现
// $queue = array();
// array_push($queue,$node);
//
// while(!is_null($node = array_shift($queue))){
// echo $node->key.' ';
// if(!is_null($node->left)){
// array_push($queue,$node->left);
// }
// if(!is_null($node->right)){
// array_push($queue,$node->right);
// }
// }
$queue = new splqueue();
$queue->enqueue($node);
while(!$queue->isEmpty()){
$node = $queue->dequeue();
echo $node->key.' ';
if (!is_null($node->left)) {
$queue->enqueue($node->left);
}
if (!is_null($node->right)) {
$queue->enqueue($node->right);
}
}
}
//层次遍历
public function LevelOrder(){
// $level = $this->getdepth($this->tree->root);
// for($i = 1;$i <= $level;$i ++){
// $this->level_order1($this->tree->root,$i);
// }
$this->level_order2($this->tree->root);
}
//获取树的层数
private function getdepth($root){
if(is_null($root)){
return 0;
}
$left = getdepth($root -> left);
$right = getdepth($root -> right);
$depth = ($left > $right ? $left : $right) + 1;
return $depth;
}
说明:level_order2方法中,在使用队列的过程中,我使用的是PHP标准库SPL提供的splqueue,如果你们习惯使用数组的话,可以使用 array_push() 和array_shift() 模拟实现。
使用:
现在我们来看看客户端代码:
class Client
{
public static function Main()
{
try {
//实现文件的自动加载
function autoload($class)
{
include strtolower($class) . '.php';
}
spl_autoload_register('autoload');
$arr = array(10, 8, 12, 7, 9, 11, 13);
$tree = new Bst();
// $tree = new Avl();
// $tree = new Rbt();
$tree->init($arr);
$traverse = new traverse($tree);
$traverse->PreOrder();
// $traverse->MidOrder();
// $traverse->PostOrder();
// $traverse->LevelOrder();
} catch (Exception $e) {
echo $e->getMessage();
}
}
}
CLient::Main();
补充:
1. 在客户端中所使用的三个类 Bst、Avl、Rbt 大家可以参考前面一篇:《PHP实现绘制二叉树图形显示功能详解》
2. 为什么我推荐大家使用SPL标准库中提供的splstack和splqueue呢?这是我在某一篇文章中看到的:虽然我们可以使用传统的变量类型来描述数据结构,例如用数组来描述堆栈(Strack)– 然后使用对应的方式 pop 和 push(array_pop()、array_push()),但你得时刻小心,因为毕竟它们不是专门用于描述数据结构的 – 一次误操作就有可能破坏该堆栈。而 SPL 的 SplStack 对象则严格以堆栈的形式描述数据,并提供对应的方法。同时,这样的代码应该也能理解它在操作堆栈而非某个数组,从而能让你的同伴更好的理解相应的代码,并且它更快。原文地址:PHP SPL,遗落的宝石
3. 本文相关参考文章: 《C语言二叉树常见操作详解【前序,中序,后序,层次遍历及非递归查找,统计个数,比较,求深度】》、《Java实现二叉树的深度优先遍历和广度优先遍历算法示例》